Advanced Center for Computing and Communication, RIKEN
School of Engineering, The University of Tokyo (until September 30, 2012)
Kazuyasu Sugiyama
(Organ and Body Scale WG)

Blood flow has the functions of maintaining healthy conditions (such as hemostasis, transport of substances, removal of foreign bodies and body temperature control). For example, if a blood vessel wall is damaged, platelets adhere to the wall and form thrombi, allowing for repair of the vessel. On the other hand, overgrown thrombi caused by any factors produce vessel occlusion, resulting in cardiac or cerebrovascular diseases with a high risk of sequelae or death. Accurate prediction of normal and abnormal blood conditions by a physical computation methodology based on logical rationales contributes to advancement of treatment and drug discovery. Our research group developed an interaction analysis program that combines fluid and structure dynamic actions (the ZZ-EFSI code) with a focus on blood flow phenomena at the continuum level.

Blood contains massive amounts of blood cells that deform flexibly. In a microcirculation system with a submilimetric scale vessel, the deformability of red blood cells and the characteristics of dense particulate flow dictate blood flow functions. The laws and the principles of dynamics (the conservation law, and constitutive equations that describe viscosity and elasticity) of blood and blood cells are simple. But, the blood system involves phenomena over a wide range of the time-space domain and exhibits complicated behavior. We have developed the ZZ-EFSI code with the aim of performing large-scale computation based on simple laws and principles. To this end, we determined new equations to be implemented and reexamined the computation scheme and algorithms, without having tuned conventional interaction analysis codes, keeping in mind that we should exploit the performance of the “K computer” [1, 2].

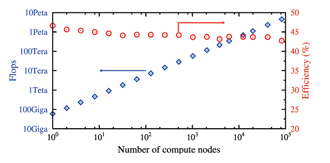
The recent scalar-type supercomputers such as the “K computer” are characterized by hierarchical parallel processing (MPI parallel computing accompanied by communication between compute nodes, thread-level parallelism between cores within compute nodes, and multiplex operation within cores). We developed an Eulerian method that does not require the process of mesh generation and reconstruction (more specifically, all physical quantities are updated on a spatially-fixed mesh). In this computing program, the rectangular computational domain is divided into meshes in the X-, Y- and Z-axis directions to describe equations and allow for MPI domain decomposition. The Eulerian method is compatible with any hardware structure at all layers and excels in expanding the scale of computation. Standard fluid applications tend to access memory too frequently with respect to the operation load. This means that a huge backlog is caused frequently in a scalar-type supercomputer that takes more time to read and write memory as compared to performing operations. The efficiency (the effective computation speed as compared to the theoretical peak performance) of the “K computer” is limited to about 10 percent. To address this issue, we developed an algorithm that requires less frequent memory access to improve the computation speed. Fig. 1 shows the performance of fluid-structure interaction analysis by the “K computer”. The efficiency as a single node was 46.6 percent, a sufficiently-high level for continuum dynamics computation by a scalar-type supercomputer. In addition, small changes in the efficiency with increase in the number of compute nodes mean high linear scalability. We performed computation of the system that contained approximately 5 million dispersed objects by using 82,944 nodes with 6.96×10¹¹ grid points, and successfully achieved an effective computation speed of 4.54 petaflops.

Fig. 1 : Weak scaling parallel performance of the ZZ-EFSI code in the “K computer” (left: effective computation speed, right: efficiency rate). The number of grid pointsper compute node is 512 × 128 × 128.

We have simulated a cerebral arteriole flow that included red blood cells and platelets (see Fig. 2 (a)). Fig. 2 (b) and (c) shows the path of some platelets. Under the condition that no red blood cells were included (Fig. 2 (b)), individual platelets had small changes in radial coordinates and moved along the vessel axis almost in a straight line. On the other hand, under the condition that red blood cells were included (Fig. 2 (c)), platelets had larger changes in radial coordinates, or in other words, dispersed easily. These results mean that red blood cells disrupt the blood flow and cause massive fluctuation of platelets, resulting in increased opportunities for platelets to approach the vessel wall. This theory is consistent with experimental results that suggest the importance of disruption effects by red blood cells against formation of platelet thrombi.

We have introduced a model of platelet adherence to a damaged vessel wall [2] and are working on a study that demonstrates experimental knowledge concerning thrombus formation. If the efficacy of drugs can be assessed based on patient-specific data in the future, it will facilitate development and discovery of new, attractive drugs. Toward this goal, we will be committed to creating models of changes in physical properties, the process of coagulation and dissolution, and biochemical reactions.

【References】
[1] BioSupercomputing Newsletter, Vol. 2, p. 11.
[2] BioSupercomputing Newsletter, Vol. 6, p. 2-3.

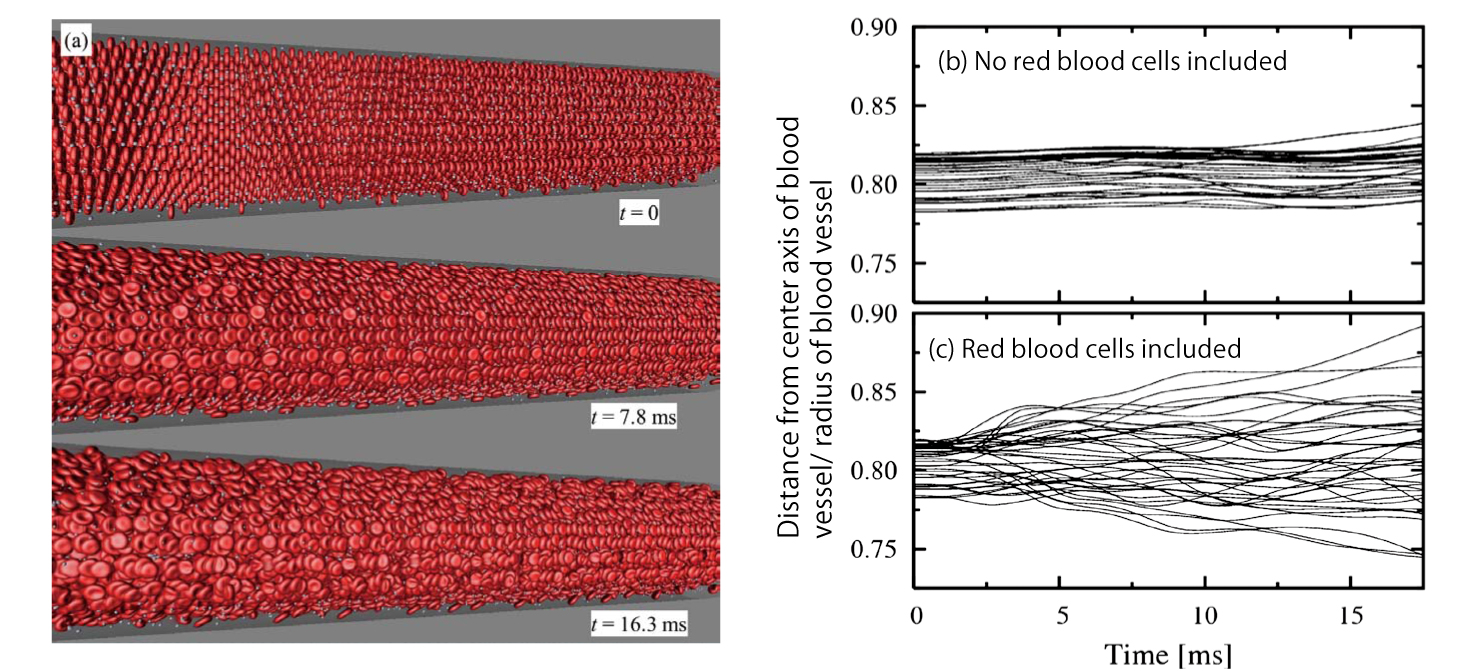
Fig. 2 : Computation results of massive dispersed objects in a blood vessel with a diameter of approximately 100 μm.
(a) Snapshots of blood cell distribution (red: red blood cells, white: platelets). Blood flows from left to right. (b) and (c) Time-varying changes of radial coordinates of platelets (meaning the distance from the center axis of the blood vessel).
The path of platelets is different depending on the presence or absence of red blood cells.