Associate Professor at School of Engineering, the University of Tokyo
(Organ and Body Scale Team)
Kazuyasu SUGIYAMA

Sixty percent of the body consists of water. Body tissues such as organs, blood vessels and blood cells are composed of soft materials. Various motions and transport phenomena, which take place autonomously and regularly throughout the body, are involved in the sustenance of life. Of these, the ones with a characteristic length of a micron-order scale or above can be considered to be the motion of a continuum and conform to the basic equations of fluid dynamics and structural dynamics. The stress characteristics of fluids and solids are mathematically expressed very differently, however. An analysis in which both of these are dealt with together and their dynamic processes are connected to each other is called a "coupled" analysis. Fluid-structure coupled simulation makes it possible to predict the effect of a treatment and help decide the treatment strategy in clinical practice. As a result, there are high expectations for its applications. It is also expected to contribute to the field of life sciences, such as in the understanding of the very essence of life and the demonstration of pathological mechanisms.

Mainly targeting industrial products, the numerical techniques of coupled analyses have been greatly developed. Based on this, many numerical studies on biomechanics are being conducted. However, it is important to further develop numerical techniques suitable for the characteristics of body tissues, which are flexible and complicated in shape, when attempting to rationalize and generalize coupled analyses.

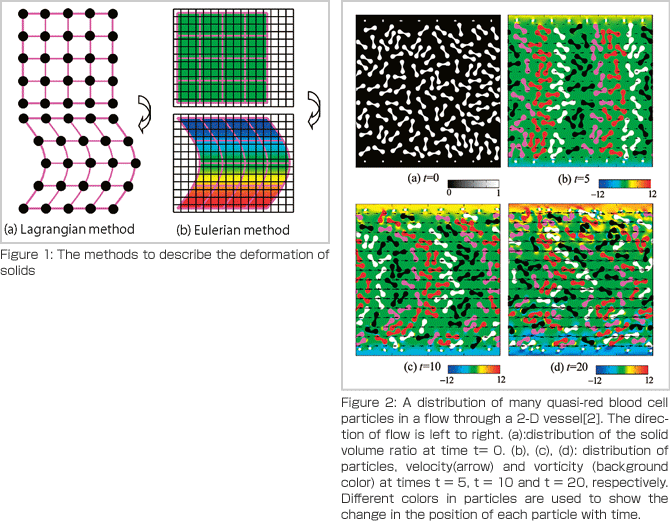
Existing structural analyses are based on the Lagrangian method in which meshes are produced according to the shape of the target and their information is updated in accordance with the deformation of the target (i.e., equations are written based on coordinates fixed to a given parcel of the target). As in the case of industrial products, if a given blueprint can provide precise information on coordinates, the generation of meshes can be automated in many cases and accurate calculations can be performed. However, a blueprint does not exist for the human body and it therefore requires the acquisition of geometric data on blood vessels and organs from medical images obtained by diagnostic equipment such as CT and MRI, before meshes are produced. As the shape of a target becomes more complicated or the size of the system used in computation becomes larger, the automation of mesh production will become more difficult. To enable coupled analysis based on each patient’s medical images to be commonly used in clinical practice, the analysis technique should be accessible even without a specialist or expertise on mesh generation.

The Organ and Body Scale Team is developing a coupled analysis technique based on the Eulerian method, in which the process of mesh production is not required (i.e., equations are written based on coordinates fixed in a space)[1]. Our approach to this development is the formulation of basic equations. For example, in the Lagrangian method, the magnitude of deformation of solids can be quantified by the relative change in coordinates of the adjacent material points after the passage of time from the starting point to the present (Figure 1 (a)). In the Eulerian method, on the other hand, the trajectory of a given material points is not tracked and therefore, some inventiveness is needed for the quantification. We define a tensor quantity that describes the deformation on each mesh. By solving its transport equation, the magnitude of deformation of solids is determined (Figure 1 (b)).

Figure 2 shows an example of Eulerian analysis, which deals with a target containing many particles[2]. If the Lagrangian method is used for the analysis of a system in which the boundary between fluid and solid changes with time, it requires a great effort to generate and reconstruct meshes. On the other hand, the use of the Eulerian method, which needs neither mesh generation nor reconstruction, makes it easily possible to perform a coupled analysis (Figure 2 (a), (b), (c)) even on a target with a complicated boundary, if the distribution of the solid volume fraction (the volume ratio of solid per mesh) at the starting point (Figure 2 (a)) is obtained.

Large-scale computation is essential when a realistic system is analyzed. A characteristic of the Eulerian analysis is to make it easily possible to perform a coupled analysis using general computational algorithms for incompressible fluid flow. For parallelization, the expertise that has been cultivated in the field of computational fluid dynamics can be utilized, which becomes a huge advantage in the realization of massively parallel computation. The introduction of this analysis method into the nextgeneration supercomputer and the consequent performance of massively parallel computation can have an incalculable impact on the field of biomechanics. For example, the expansion of the scale and models of computation in Figure 2 allows us to analyze a series of phenomena starting from the adsorption of platelets through the development of blood clots until their detachment, under a condition in which many red blood cells are present. It is expected that the effect of dynamics in thrombosis will be better understood.

References
[1] Shu Takagi (2009) "Simulation of the human body using the nextgeneration supercomputer (in Japanese)," Sugaku Seminar, 48, 58-64.
[2] Sugiyama, K., Ii, S., Takeuchi, S., Takagi, S. and Matsumoto, Y. (2010) "Full Eulerian simulations of biconcave neo-Hookean particles in a Poiseuille flow," Comput. Mech. (accepted).